接着昨天的分析。
已经发现在纬线上的偏移值呈现出明显的规律性,这个规律不难拟合出来。利用拟合出来的函数将这个高频扰动抵消之后,得到了这样的曲线:
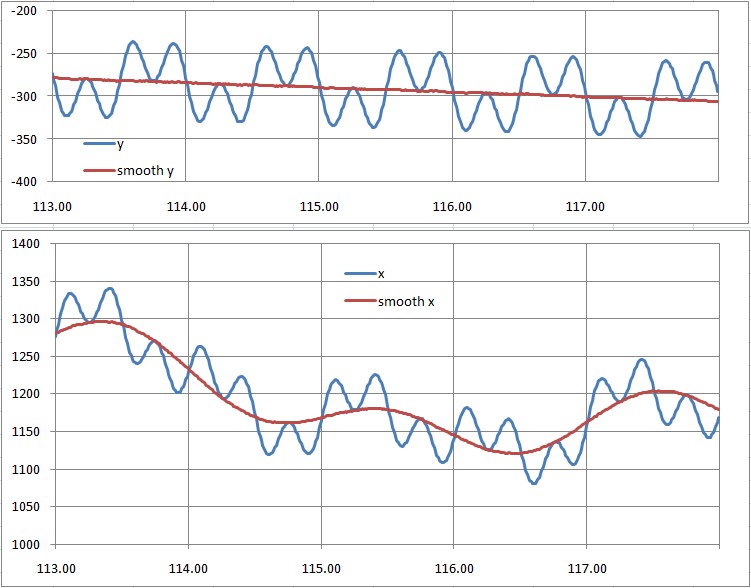
看起来相当完美。那在看看将它应用到大尺度上效果如何:
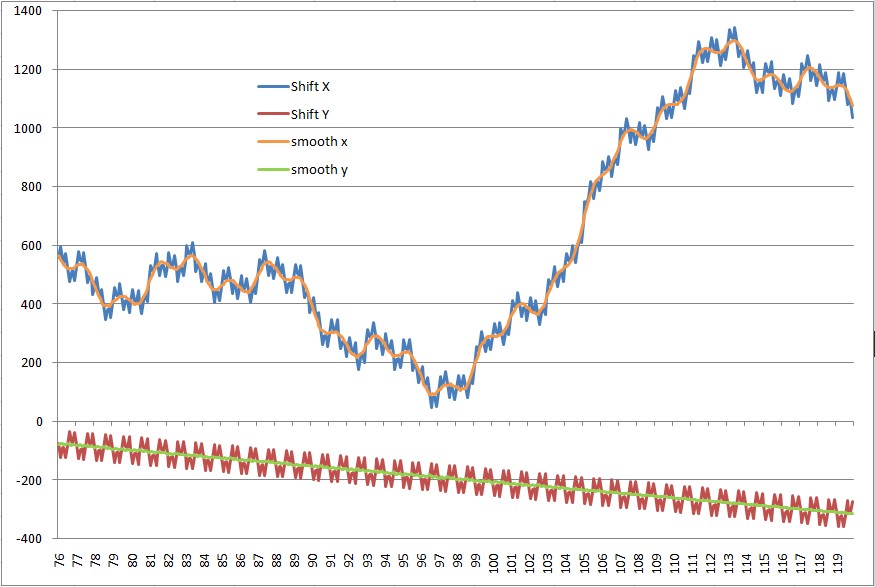
有微小的抖动,看来参数细节还需要微调一下,不过要求不高的话其实已经可以接受了。
接下来,在这张图上又发现了规律…… 嗯,我不能继续写下去了。
其实对于离线应用,进一步的分析不做也没有关系了,并不需要将整个函数拟合出来,剩余的工作可以通过查表法来做,然后插值再加回高频扰动。因为知道了高频扰动的函数后,就能够用较低的采样频率来记录偏移量,即使将整个表放内存里,占用的空间大小也可以接受。